Wie mißt man Entfernungen auf See und auf dem Lande? Wenn man auf einem Berg oder auf einem hohen Gebäude steht, sieht man ebenso weit wie einst der phönizische Matrose hoch im Krähennest auf dem Mast.
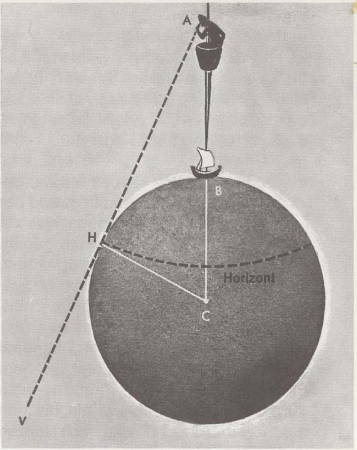
Wir zeichnen die Erdkugel und darauf übertrieben groß einen Mann im Krähennest, wie er Umschau hält, soweit er sehen kann. Auf der Zeichnung ist der Mann Punkt A. Seine Höhe über der Erde ist dann AB. Die Linie BC ist der Erdradius, eine Linie vom Mittelpunkt bis an die Oberfläche. Sie ist rund 6368 Kilometer lang. Der Mann blickt entlang der Linie AHV bis zu dem Punkt H, an dem sich der Himmel und das Meer zu treffen scheinen. Nur an diesem Punkt berührtdie Linie die Erde. Wenn er rund um sich blickt, soweit er sehen kann, bilden diese Berührungspunkte zusammen auf derErdkugel einen Kreis. Diese Kreislinie nennt man Horizont. (Einen so großen Teil der Erde, wie ihn die hier eingezeichnete Horizontlinie angibt, siehtein Mann in Wirklichkeit erst, wenn er sich mehrere tausend km von der Erde entfernt in einem Satelliten befindet.) Will der Seemann die Entfernung zum Horizont messen, so gebraucht er die mathematische Formel d = 2,081 mal √h. Hier bedeutet d die Entfernung zum Horizont in Seemeilen und h die Höhe über der Meeresoberfläche in Metern. Versuchen wir ein Beispiel:
Der Mann befindet sich im Mastkorb eines Schiffes 9 Meter über der Meeresoberfläche. Wie weit ist der Horizont entfernt? Wir gebrauchen die Formel 2,081 · √9. Die Quadratwurzel von 9 ist 3 (3 • 3 = 9). Unsere Antwort lautet also 2,081 • 3 = 6,243 Seemeilen oder, da eine Seemeile = 1,852 Kilometer ist, 6,243 • 1,852 = 11,562 Kilometer.