Hoe afstanden te meten op zee en op het land?? Wanneer u op een berg of op een hoog gebouw staat, kan worden gezien zo ver als de Fenicische zeelieden ooit hoog in het kraaiennest op de mast deden.
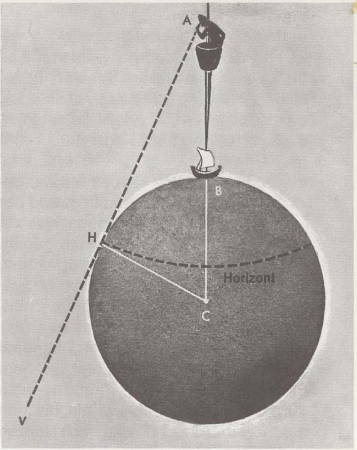
We tekenen de wereldbol en daarop, overdreven groot, een man in een kraaiennest, hoe hij om zich heen kijkt, voor zover hij kan zien. Op de tekening is de man punt A. De hoogte boven de aarde is dan AB. De lijn BC is de straal van de aarde, een lijn van het midden naar het oppervlak. Ze is rond 6368 Kilometers lang. De man kijkt langs de lijn AHV naar punt H, waar de lucht en de zee elkaar lijken te ontmoeten. Alleen op dit punt raakt de lijn de aarde. Als hij om zich heen kijkt, voor zover hij kan zien, deze contactpunten vormen samen een cirkel op de aardbol. Deze cirkelvormige lijn wordt de horizon genoemd. (Zo'n groot deel van de aarde, zoals aangegeven door de hier getekende horizonlijn, een man ziet het eerst in de werkelijkheid, wanneer het zich in een satelliet enkele duizenden kilometers van de aarde bevindt.) Wil de zeeman de afstand tot de horizon meten?, dus gebruikt hij de wiskundige formule d = 2,081 mal h. Hierin is d de afstand tot de horizon in zeemijlen en h is de hoogte boven zeeniveau in meters. Laten we een voorbeeld proberen:
De man is in de masttop van een schip 9 meter boven het zeeoppervlak. Hoe ver is de horizon?? We gebruiken de formule 2,081 · √9. De vierkantswortel van 9 is 3 (3 • 3 = 9). Dus ons antwoord is: 2,081 • 3 = 6,243 nautische mijlen of, omdat een zeemijl = 1,852 kilometer is, 6,243 • 1,852 = 11,562 Kilometer.