Comment mesurer les distances en mer et sur terre? Lorsque vous vous tenez sur une montagne ou sur un grand bâtiment, peut être vu aussi loin que les marins phéniciens le faisaient autrefois haut dans le nid de pie sur le mât.
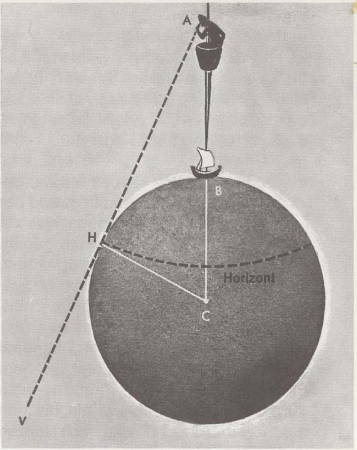
On dessine le globe et dessus, exagérément grand, un homme dans un nid de pie, comment il regarde autour de lui, aussi loin qu'il puisse voir. Sur le dessin, l'homme est le point A. Sa hauteur au-dessus de la terre est alors AB. La ligne BC est le rayon de la terre, une ligne du centre à la surface. elle est ronde 6368 Kilomètres de long. L'homme regarde le long de la ligne AHV jusqu'au point H, où le ciel et la mer semblent se rencontrer. Ce n'est qu'à ce point que la ligne touche la terre. Quand il regarde autour de lui, aussi loin qu'il puisse voir, ces points de contact forment ensemble un cercle sur le globe. Cette ligne circulaire s'appelle l'horizon. (Une si grande partie de la terre, comme indiqué par la ligne d'horizon tracée ici, un homme voit d'abord en réalité, lorsqu'il est à plusieurs milliers de km de la Terre dans un satellite.) Le marin veut-il mesurer la distance à l'horizon, il utilise donc la formule mathématique d = 2,081 mal √h. Ici d est la distance à l'horizon en miles nautiques et h est la hauteur au-dessus du niveau de la mer en mètres. Essayons un exemple:
L'homme est dans la tête de mât d'un navire 9 mètres au-dessus de la surface de la mer. A quelle distance est l'horizon? Nous utilisons la formule 2,081 · √9. La racine carrée de 9 est 3 (3 • 3 = 9). Alors notre réponse est 2,081 • 3 = 6,243 milles nautiques ou, car un mille marin = 1,852 kilomètres est, 6,243 • 1,852 = 11,562 Kilomètre.