egyptisk, Babylonier och greker använde kulramen före romarna. Kineserna och japanerna kände också till sådana enkla räknemaskiner. Kulramen används än idag i Kina och Japan, och de få, som fortfarande använder det, är så bra med det, att de kan lösa problem nästan lika snabbt som en elektrisk miniräknare. Kulramen har kommit i många former och under olika namn, beroende på, när och var det behövdes, men tillvägagångssättet var alltid detsamma i princip. Den har enstaka rader av glaspärlor, tallrikar eller bollar, och dessa serier är ordnade efter platsvärdessystemet, som sumererna uppfann. Den tidigaste och enklaste kulramen var en räknebräda, användes av de babyloniska köpmännen.
Ett 263 och 349 tillägga, vi lägger stenar på tavlan så här, att hon 263 betyda: 2 hundratals, 6 tiotals och 3 ett. Vi lägger sedan till stenar,
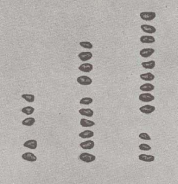de 349 specificera: 3 hundratals, 4 tiotals och 9 ett.
Eftersom ingen rad mer än 9 kan ha stenar (10 en = 1 tiotals), låt oss ta först 9 Stenar från ena raden (rätt) bort, sedan tar vi den tionde och lägger den i raden om tio. Det finns nu två stenar kvar i enraden.
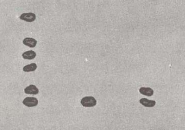
Men i tiotal (mellersta raden) är också mer än 9 stenar. Man tar igen här 9 Stenar bort och sätter den tionde i hundraraden (länkar). Nu ger stenarna svaret: 612.
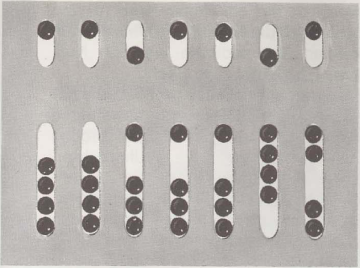
Den romerska räknebrädan, kulramen, var metall, och i varje rad låg små bollar. För att beteckna ett nummer, bollarna sköts mot mitten. Bollarna ovan var värda 5, den nedre av 1. Den första raden till höger är en-, den andra raden av tio och så vidare. Antalet som visas är enligt vårt räknesystem: 0061 192 = 61 192. I Asien kallades kulramen "suan-pan" av kineserna och "soro-ban" av japanerna. Glasbitarna på ramens avdelarskena bildar ett nummer, Vår illustration visar, som numret 651 är skrivet: !n raden av hundra är en överst 5 och en nedan 1, i
rad om tio en 5 och på en rad ett 1.
Vi vill nu 152 till 651 tillägga. Vi trycker först 2 Ett stycke till delningsskenan (höger rad). Ett 5 att lägga till tiotalsserien, vi skjuter upp alla fyra nedre glasbitarna. Eftersom vi, a 10 att få tior, behöver en till glasbit, men har inga fler i den här raden, låt oss trycka bort alla tiotals glasbitar från skiljelinjen och i hundratalsraden trycka en glasbit underifrån till skiljelinjen. Slutligen sätter vi in i hundra raden 1 glasbit upp, och glasbitarna ger resultatet: 803.
