egyptisk, Babyloniere og grækere brugte abacus før romerne. Kineserne og japanerne kendte også sådanne simple tællemaskiner. Abacusen bruges stadig i dag i Kina og Japan, og de få, som stadig bruger det, har det så godt med det, at de kan løse problemer næsten lige så hurtigt som en elektrisk lommeregner. Kulerammen er kommet i mange former og under forskellige navne, er efter, hvornår og hvor det var nødvendigt, men fremgangsmåden var i princippet altid den samme. Den har enkelte rækker af glasperler, tallerkener eller kugler, og disse serier er arrangeret efter stedværdisystemet, som sumererne opfandt. Den tidligste og enkleste kuleramme var et tællebræt, brugt af de babylonske købmænd.
En 263 og 349 at tilføje, vi sætter sten på tavlen sådan her, at hun 263 betyde: 2 hundredvis, 6 tiere og 3 en. Vi tilføjer derefter sten,
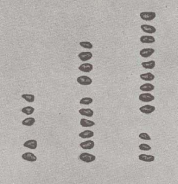det 349 specificere: 3 hundredvis, 4 tiere og 9 en.
Da ingen række mere end 9 kan have sten (10 en = 1 tiere), lad os tage først 9 Sten fra den ene række (ret) væk, så tager vi den tiende og sætter den i rækken af ti. Der er nu to sten tilbage i den ene række.
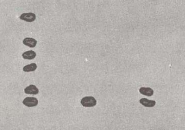
Men i tiere (midterste række) er også mere end 9 sten. Man tager igen her 9 Sten væk og sæt den tiende i hundrederækken (links). Nu giver stenene svaret: 612.
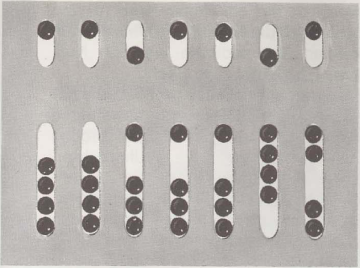
Det romerske tællebord, abacusen, var metal, og i hver række var der små kugler. For at angive et tal, boldene blev skubbet ind mod midten. Boldene ovenfor var værd 5, den nederste af 1. Den første række til højre er den ene-, den anden rækken af ti og så videre. Det viste tal er i henhold til vores tællesystem: 0061 192 = 61 192. I Asien blev abacus kaldt "suan-pan" af kineserne og "soro-ban" af japanerne. Glasstykkerne på rammens skilleskinne danner et tal, Vores illustration viser, ligesom nummeret 651 er skrevet: !n rækken af hundreder er en øverst 5 og en nedenfor 1, i
række af ti en 5 og i den ene række 1.
Vi vil nu 152 til 651 at tilføje. Vi presser først 2 Et stykke til skilleskinnen (højre række). En 5 at tilføje til tierrækken, vi skubber alle fire nederste stykker glas op. Siden vi, renovation 10 at få tiere, skal bruge endnu et stykke glas, men har ikke flere i denne serie, lad os skubbe alle 10 glasstykker væk fra skillelinjen og i hundrederækken skubbe et glasstykke nedefra til skillelinjen. Til sidst indsætter vi i hundredrækken 1 stykke glas op, og glasstykkerne giver resultatet: 803.
