Egyptische, Babyloniërs en Grieken gebruikten het telraam vóór de Romeinen. De Chinezen en Japanners kenden ook zulke simpele telmachines. Het telraam wordt nog steeds gebruikt in China en Japan, en de weinigen, wie gebruikt het nog?, ben er zo goed in, dat ze problemen bijna net zo snel kunnen oplossen als een elektrische rekenmachine. Het telraam is er in vele vormen en onder verschillende namen, is na, wanneer en waar het nodig was, maar de procedure was in principe altijd hetzelfde. Het heeft enkele rijen glaskralen, borden of ballen, en deze reeksen zijn gerangschikt volgens het plaatswaardesysteem, dat de Sumeriërs hebben uitgevonden. Het vroegste en eenvoudigste telraam was een telbord, gebruikt door de Babylonische kooplieden.
een 263 en 349 toevoegen, we leggen stenen zo op het bord, dat zij 263 gemeen: 2 honderden, 6 tientallen en 3 een. We voegen dan stenen toe,
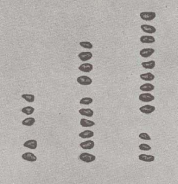de 349 specificeren: 3 honderden, 4 tientallen en 9 een.
Aangezien geen rij meer dan 9 kan stenen hebben (10 een = 1 tientallen), laten we eerst nemen 9 Stenen uit de ene rij (Rechtsaf) weg, dan nemen we de tiende en plaatsen deze in de rij van tien. Er zijn nu nog twee stenen in de ene rij.
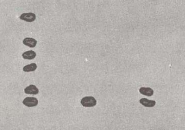
Maar in de tientallen (middelste rij) zijn ook meer dan 9 stenen. Men neemt weer hier 9 Stenen weg en zet de tiende in de honderd rij (links). Nu geven de stenen het antwoord: 612.
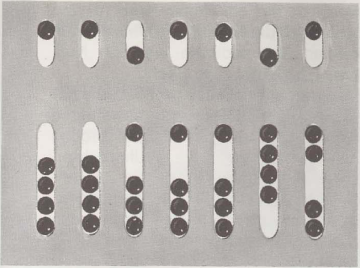
Het Romeinse telbord, het telraam, was metaal, en in elke rij waren kleine balletjes. Om een getal aan te duiden, de ballen werden naar het midden geduwd. De ballen hierboven waren de moeite waard 5, de laagste van 1. De eerste rij rechts is de een-, de tweede de rij van tien enzovoort. Het getoonde aantal is volgens ons telsysteem: 0061 192 = 61 192. In Azië werd het telraam door de Chinezen "suan-pan" en door de Japanners "soro-ban" genoemd.. De stukjes glas op de scheidingsrail van het frame vormen een nummer, Onze illustratie toont:, vind het nummer leuk 651 is geschreven: !n de rij van honderden is er één bovenaan 5 en een hieronder 1, in de
rij van tien een 5 en in de ene rij een 1.
We willen nu 152 naar de 651 toevoegen. Wij duwen eerst 2 Een stuk aan de scheidingsrail (rechter rij). een 5 om toe te voegen aan de reeks van tientallen, we schuiven alle vier de onderste stukken glas omhoog. Sinds we, a 10 tienen krijgen, nog een stuk glas nodig, maar heb er geen meer in deze serie, laten we alle tientallen stukjes glas wegduwen van de scheidslijn en in de honderden rij duwen we een stuk glas van onder naar de scheidslijn. Eindelijk voegen we in de honderd rij in 1 stuk glas omhoog, en de stukjes glas geven het resultaat: 803.
