Ägypter, Babylonier und Griechen gebrauchten das Rechenbrett schon vor den Römern. Solche einfache Zählmaschine kannten auch die Chinesen und Japaner. Selbst heute noch wird in China und Japan das Rechenbrett gebraucht, und die wenigen, die es noch verwenden, sind so geschickt damit, daß sie Aufgaben fast so schnell lösen können wie eine elektrische Rechenmaschine. Das Rechenbrett hat es zwar in vielen Formen und unter verschiedenen Namen gegeben, je nachdem, wann und wo es gebraucht wurde, aber das Verfahren war im Prinzip stets das gleiche. Es hat einzelne Reihen von Glasperlen, Plättchen oder Kugeln, und diese Reihen sind nach dem Stellenwertsystem angeordnet, das die Sumerer erfanden. Das früheste und einfachste Rechenbrett war ein Zählbrett, das von den babylonischen Kaufleuten gebraucht wurde.
Um 263 und 349 zu addieren, setzen wir Steine so auf das Brett, daß sie 263 bedeuten: 2 Hunderter, 6 Zehner und 3 Einer. Wir fügen dann Steine hinzu,
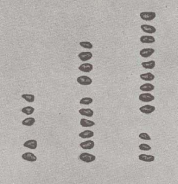die 349 angeben: 3 Hunderter, 4 Zehner und 9 Einer.
Da keine Reihe mehr als 9 Steine haben kann (10 Einer = 1 Zehner), nehmen wir zuerst 9 Steine von der Einer-Reihe (rechts) weg, dann nehmen wir den zehnten und legen ihn in die ZehnerReihe. In der Einer-Reihe bleiben nun zwei Steine übrig.
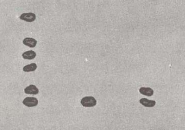
Aber in der Zehner-Reihe (mittlere Reihe) sind auch mehr als 9 Steine. Man nimmt auch hier wieder 9 Steine weg und legt den zehnten in die HunderterReihe (links). Jetzt geben die Steine die Antwort: 612.
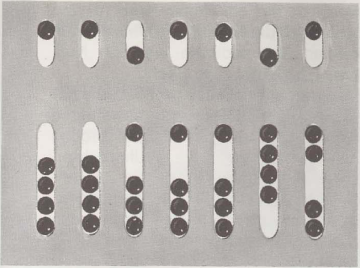
Das römische Zählbrett, der Abakus, war aus Metall, und in jeder Reihe befanden sich kleine Kugeln. Um eine Zahl zu bezeichnen, wurden die Kugeln an die Mitte herangeschoben. Die Kugeln oben hatten den Wert von 5, die unteren von 1. Die erste Reihe rechts ist die Einer-, die zweite die Zehner-Reihe und so fort. Die dargestellte Zahl ist nach unserem Zahlsystem: 0061 192 = 61 192. In Asien wurde das Rechenbrett von den Chinesen „suan-pan“ und von den Japanern „soro-ban“ genannt. Die Glasstücke an der Trennschiene des Rahmens bilden eine Zahl, Unsere Abbildung zeigt, wie die Zahl 651 geschrieben wird: !n der Hunderter-Reihe ist oben eine 5 und unten eine 1, in der
Zehner-Reihe eine 5 und in der Einer-Reiheeinel 1.
Wir wollen nun 152 zu den 651 hinzuzählen. Wir schieben zunächst 2 Einerstücke an die Trennschiene (rechte Reihe). Um 5 zur Zehner-Reihe zu addieren, schieben wir alle vier unteren Glasstücke nach oben. Da wir, um 10 Zehner zu bekommen, noch ein Glasstück brauchen, aber in dieser Reihe keines mehr haben, schieben wir alle Zehner-Glasstücke vom Trennstrich weg und schieben in der HunderterReihe ein Glasstück von unten an die Trennlinie. Zuletzt schieben wir in der Hunderter-Reihe noch ein 1 Glasstück nach oben, und die Glasstücke geben das Resultat: 803.
