Mål haven

Hvem har en rektangulær have, han har det ret let med at måle. Han måler simpelthen længden og bredden af ​​sin ejendom. Dette giver ham ikke kun sidemålene, men når du gange begge sider, så får du området, at du kan arbejde som gartner:

Følgende gælder for en forholdsvis jævnt firkantet grund:

Lang x bredde = samlet areal

Hvorfor har du egentlig brug for det samlede areal?

Hvem vil lave en rigtig haveplan, han burde gøre det i skala. Vil du spare dig selv for dette arbejde af tids- eller bekvemmelighedshensyn?, så vil du hurtigt bemærke det, at dette ikke er en god løsning. En rimelig plan kan ikke udarbejdes med oplysninger som "groft". Med en ny- eller ombygning af en have, det er også meget nyttigt, fordi du deler ejendommen op i individuelle net. Det er selvfølgelig kun muligt, hvis du på forhånd har fastlagt de nøjagtige dimensioner.

Men hvad laver de, der ønsker at måle en uregelmæssig have?

Med en grund, der ikke har en normal firkantet form, man kan nøjes med dele.

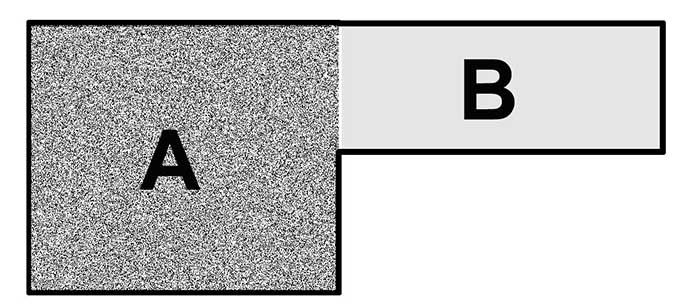
Die L-form

Du deler simpelthen en L-formet have i to firkanter og beregner hver enkelt for dig selv. Derefter tilføjes områderne, og du har også præcise oplysninger her.

Flere uregelmæssige former

For at gøre dit arbejde og regning lettere, man bør forsøge at finde en slags regelmæssighed i alle uregelmæssige dimensioner, som derefter let kan beregnes. En have med et punkt kunne måles sådan:

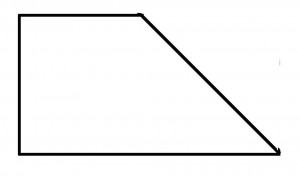
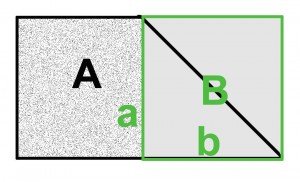
Samlet areal = areal A plus halveret areal B

Hvis dette eksempel heller ikke passer, så kan du prøve at opdele haven i yderligere beregningsbare dele.

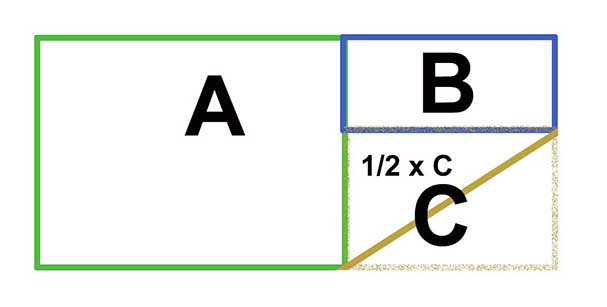
Pythagoras nej tak?

Hvem spurgte i skolen, hvorfor han skulle have brug for den pythagoranske sætning og lignende i livet, svaret får han senest med sådan en ejendom.

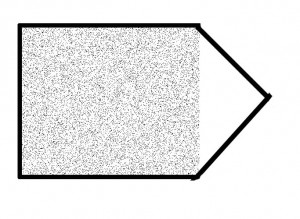
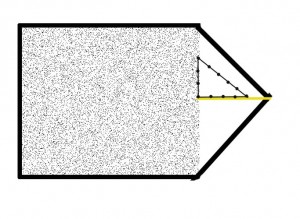
Den ene side måles her (g) arealet, der skal beregnes og, baseret på dette, i en ret vinkel en afstand til toppen af ​​haven (h). Nu mangler der kun formlen for arealet af en trekant. Det siger: A = ½ g x h.

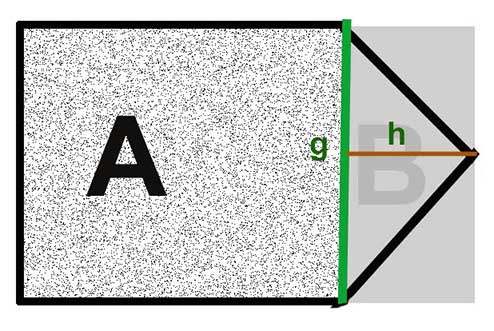
Det betyder for denne sag: Arealet af toppen af ​​haven beregnes som følger:

Længden af ​​basen gange højden af ​​trekanten (ret vinkel til spidsen) delt med to

Det lyder kompliceret - men det er ikke så slemt.

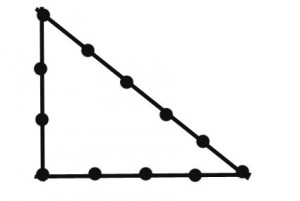
Men hvordan laver man den rigtige vinkel??

At konstruere en ret vinkel i haven, mangler bare en længere ledning. I dette tilfælde med intervaller på 1 Målermærker vedhæftet. Samlet set har du brug for 13 knudepunkt. Nodenummer 1 danner begyndelsen. Det er fastgjort til jorden med et stort søm. Nu spænder du ledningen sådan, at du får en trekant, som er kantlængderne på 3, 4 og 5 Meter (så knudepunkter) hat. Nodenummer 13 kommer ned til det nøjagtige antal 1. Den rigtige vinkel skabes mellem de to kortere sider af trekanten. I øvrigt er dette Pythagoras sætning i praktisk anvendelse.