Mät trädgården
Som har en rektangulär trädgård, han har det ganska enkelt med att mäta. Han mäter helt enkelt längden och bredden på sin egendom. Detta ger honom inte bara sidodimensionerna, men när du multiplicerar båda sidor, då får du området, att du kan arbeta som trädgårdsmästare:
Följande gäller för en relativt jämnt kvadratisk tomt:
Lång x bredd = total yta
Varför behöver du egentligen den totala ytan?
Vem vill skapa en riktig trädgårdsplan, han borde göra det i skala. Vill du spara dig själv detta arbete av tidsskäl eller bekvämlighet?, då märker du snabbt, att detta inte är en bra lösning. En rimlig plan kan inte upprättas med information som "grovt". Med en ny- eller ombyggnad av en trädgård, det är också mycket hjälpsamt, eftersom du delar fastigheten i enskilda rutnät. Naturligtvis är det bara möjligt, om du har bestämt de exakta måtten i förväg.
Men vad gör de, som vill mäta en oregelbunden trädgård?
Med en tomt, som inte har en vanlig fyrkantig form, man kan nöja sig med delar.
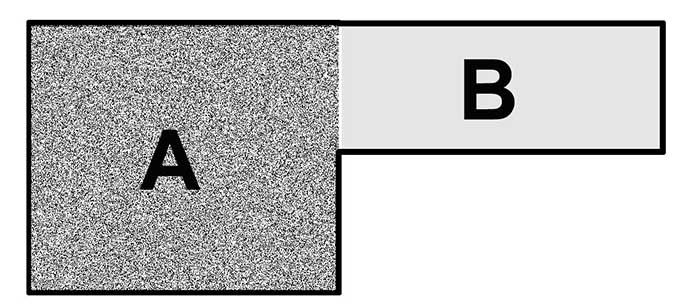
Die L-Form
Du delar helt enkelt upp en L-formad trädgård i två rutor och beräknar var och en för dig själv. Sedan läggs områdena ihop och du har exakt information också här.
Mer oregelbundna former
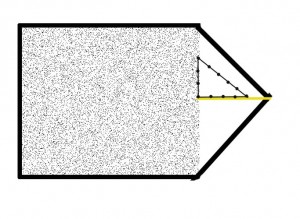
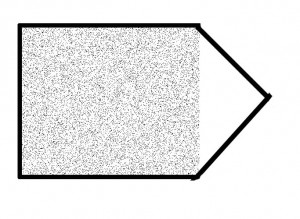
För att göra ditt arbete och aritmetik enklare, man bör försöka hitta en sorts regelbundenhet i alla oregelbundna dimensioner, som sedan enkelt kan beräknas. En trädgård med en spets kunde mätas så här:
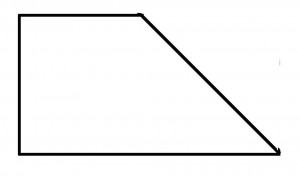
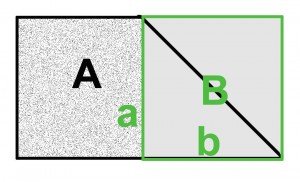
Total yta = yta A plus halverad yta B
Om det här exemplet inte passar heller, då kan du försöka dela upp trädgården i ytterligare beräkningsbara delar.
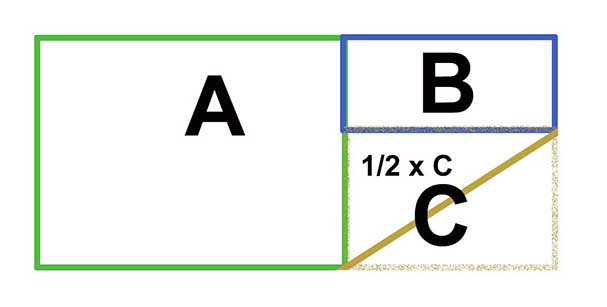
Pythagoras nej tack?
Vem frågade i skolan, varför han skulle behöva Pythagoras sats och liknande i livet, han får svaret senast med en sådan egendom.
En sida mäts här (g) området som ska beräknas och, baserat på detta, i rät vinkel ett avstånd till toppen av trädgården (h). Nu saknas bara formeln för arean av en triangel. Det står: A = ½ g x h.
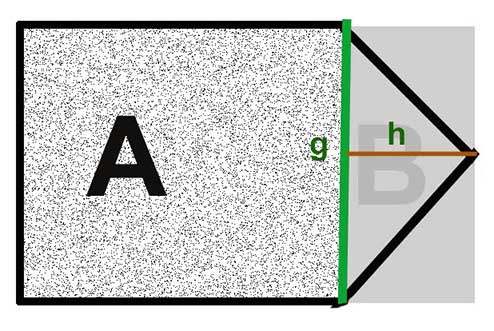
Det betyder för detta fall: Ytan på toppen av trädgården beräknas enligt följande:
Basens längd gånger triangelns höjd (rätt vinkel mot spetsen) delat med två
Låter komplicerat - men det är inte så illa.
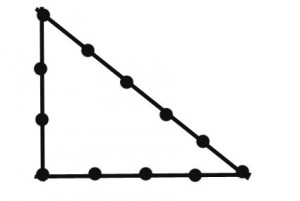
Men hur gör man en rätt vinkel??
Att konstruera en rät vinkel i trädgården, behöver bara en längre sladd. I det här fallet, med intervaller av 1 Mätarmarkeringar bifogade. Sammantaget behöver du 13 nod. Nodnummer 1 utgör början. Den är fäst vid marken med en stor spik. Nu spänner du sladden så här, att du får en triangel, som är kantlängderna på 3, 4 och 5 Mätare (så nodavstånd) hatt. Nodnummer 13 kommer ner till det exakta antalet 1. Rätt vinkel skapas mellan de två kortare sidorna av triangeln. För övrigt är detta Pythagoras sats i praktisk tillämpning.