De hier getoonde methode kan worden toegepast op magische vierkanten van elke grootte, mits ze een oneven aantal horizontale en verticale rijen hebben. Dus laten we eerst het nummer schrijven 1 in het midden van de bovenste rij. Nu gaan we diagonaal naar rechtsboven met het potlood en zijn dus buiten het vierkant. Dus we gaan de volgende rij naar het laatste vierkant en schrijven het nummer 2 in. Laten we nu nog een stap diagonaal naar boven en naar rechts doen, we zijn weer van het plein af. {Met het vijfkwadraat zouden we hier een veld hebben, om de 3 in te schrijven.) Dus we gaan de rij naar links naar het laatste veld en stellen het nummer in 3 in.
We hebben nu de eerste reeks getallen geschreven. Een reeks getallen is gelijk aan het aantal longitudinale- of rijen kruisen, in dit geval 3. Om de volgende zin uit te lijnen, laten we een vakje naar beneden gaan en het eerste cijfer van de tweede zin schrijven, 4. (Het eerste cijfer van de volgende zin staat altijd onder het laatste cijfer van de vorige zin.) We herhalen nu dezelfde procedure als in het eerste deel: één veld diagonaal naar rechtsboven, 5, en verder schuin naar rechtsboven, 6. Hiermee is de tweede zin voltooid. We gaan van de 6 een ander veld in, schrijven 7 in en voltooi het vierkant op dezelfde manier als voorheen.
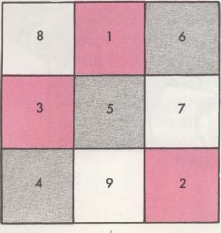Hoe maak je een magisch vierkant?, De velden voor de eerste "Zin"” Cijfers zijn rood, grijs voor de tweede set en wit voor de derde set.