Pokazaną tutaj metodę można zastosować do magicznych kwadratów o dowolnym rozmiarze, pod warunkiem, że mają nieparzystą liczbę rzędów poziomych i pionowych. Więc najpierw napiszmy numer 1 w środku górnego rzędu. Teraz idziemy ołówkiem po przekątnej w prawo w górę iw ten sposób wychodzimy poza kwadrat. Przechodzimy więc w następnym rzędzie do ostatniego kwadratu i wpisujemy liczbę 2 w. Teraz zróbmy kolejny krok po przekątnej w górę i w prawo, znowu wychodzimy z placu. {Z pięcioma kwadratami mielibyśmy tutaj pole, napisać 3 cale) Przechodzimy więc wierszem w lewo do ostatniego pola i ustawiamy liczbę 3 w.
Napisaliśmy teraz pierwszy zestaw liczb. Zbiór liczb jest równy liczbie podłużnej- lub skrzyżować rzędy, w tym przypadku 3. Aby wyrównać następne zdanie, zejdźmy o jeden kwadrat w dół i napiszmy pierwszą cyfrę drugiego zdania, 4. (Pierwsza cyfra następnego zdania jest zawsze pod ostatnią cyfrą poprzedniego zdania.) Powtarzamy teraz tę samą procedurę, co w części pierwszej: jedno pole po przekątnej w prawym górnym rogu, 5, i dalej po przekątnej w prawym górnym rogu, 6. To kończy drugie zdanie. Idziemy od 6 w dół innego pola, pisać 7 i uzupełnij kwadrat w taki sam sposób jak poprzednio.
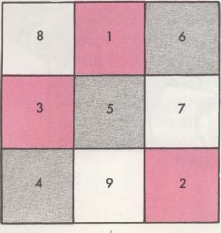Jak zrobić magiczny kwadrat, Pola dla pierwszego „Zdanie” Liczby są czerwone, szary dla drugiego seta i biały dla trzeciego seta.