UNE. Désignations
- Tous montants: UNE, B, C, M, ….
2. orthographes et définitions
B. Relations entre ensembles
* La notation A ⊆ B est également équivalente
C. Opérations avec des ensembles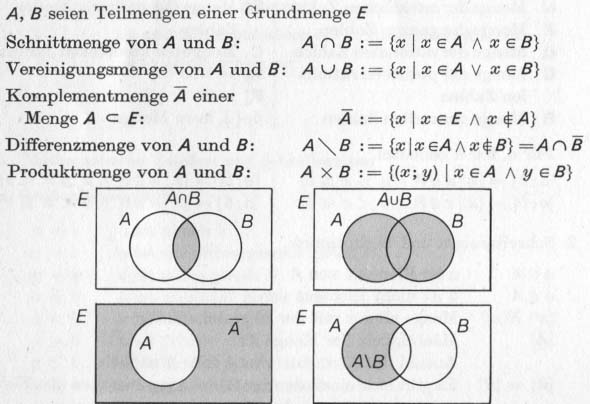
ré. Lois de l'algèbre des ensembles
UNE, B, C sont des sous-ensembles d'un ensemble de base E
principe de dualité: Si on intervertit les opérations ∩ et U et en même temps Ø et E dans une loi d'algèbre ensembliste, cela se traduit à nouveau par une loi de l'algèbre des ensembles.
E. classification (démontage) beaucoup
Il existe un classement, lorsqu'un ensemble est divisé en sous-ensembles, pour que
(1) chaque sous-ensemble contient au moins un élément,
(2) l'intersection de deux sous-ensembles est vide,
(3) l'union de tous les sous-ensembles donne l'ensemble original.